GLOSARIO MATEMÁTICO
1. Método sustitución:
Para resolver sistemas de ecuaciones lineales existen tres métodos diferentes: el de sustitución, el de igualación y el de reducción. Aquí va el primero. El método de sustitución consiste en despejar la en una de las ecuaciones, básicamente en la que resulte más fácil, y sustituir la expresión resultante en la otra.

2. Método de igualación:
Método de igualación. El método de igualación, consiste en despejar la misma incógnita en ambas ecuaciones e igualar las expresiones obtenidas.

3. Método de reducción:
Método de reducción. ... Normalmente, elegimos este método cuando una de las incógnitas tiene el mismo coeficiente, pero de signo distinto, en ambas ecuaciones. El método de reducción consiste en operar con las ecuaciones como, por ejemplo, sumar o restar ambas ecuaciones, de modo que una de las incógnitas desaparezca.

4. Método de determinantes:
La regla de Cramer se aplica para resolver sistemas de ecuaciones lineales que cumplan las siguientes condiciones: 1 El número de ecuaciones es igual al número de incógnitas. 2 El determinante de la matriz de los coeficientes es distinto de cero.
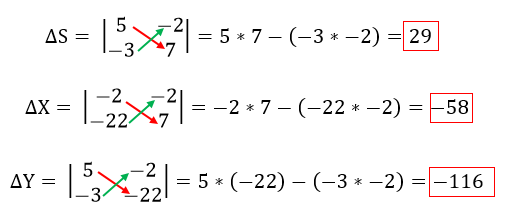
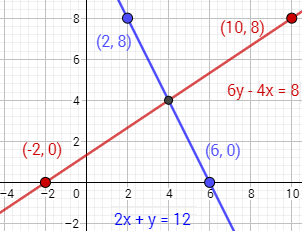
5. Método gráfico:
Consiste en representar en un sistema de coordenadas, ambas rectas y comprobar si se cortan y, si es así, dónde.
El proceso de resolución de un sistema de ecuaciones mediante el método gráfico se resume en las siguientes fases:
1. Se despeja la incógnita y en ambas ecuaciones.
2. Se construye, para cada una de las dos funciones de primer grado obtenidas, la tabla de valores correspondientes.
3. Se representan gráficamente ambas rectas en los ejes coordenados.
6. Función:
Una función matemática es una relación que se establece
entre dos conjuntos, a través de la cual a cada elemento del primer conjunto se
le asigna un único elemento del segundo conjunto o ninguno. Al conjunto inicial
o conjunto de partida también se lo llama dominio; al conjunto final o conjunto
de llegada, en tanto, se lo puede denominar codominio. Se lo representa por f(x).
7. FUNCIÓN LINEAL:

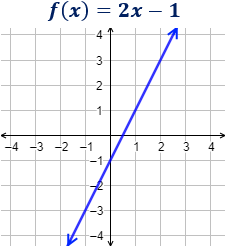 La pendiente de la función es y la ordenada es .
La pendiente de la función es y la ordenada es .
Una función lineal es una función polinómica de primer grado. Es decir, tiene la siguiente forma

siendo .
- es la pendiente de la función
- es la ordenada (en el origen) de la función
La gráfica de una función lineal es siempre una recta.
Ejemplo

8. FACTOR COMÚN
Si varios sumandos tienen un factor común, podemos transformar la suma en producto extrayendo dicho factor.
a · b + a · c = a · (b + c)
2 · 3 + 2 · 5 = 2 · (3 + 5)
6 + 10 = 2 · 8
16 = 16
a · b − a · c = a · (b − c)
2 · 5 − 2 · 3 = 2 · (5 − 3)
10 − 6 = 2 · 2
4 = 4
Sacar factor común es el proceso inverso a la propiedad distributiva.
9. Trinomio cuadrado de la forma ax2 + bx + c
Este tipo de trinomio se diferencia del anterior debido a que el termino al cuadrado (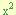 ) se encuentra precedido por un coeficiente diferente de uno (debe ser positivo). Este se trabaja de una manera un poco diferente, la cual detallamos a continuación:
) se encuentra precedido por un coeficiente diferente de uno (debe ser positivo). Este se trabaja de una manera un poco diferente, la cual detallamos a continuación:
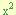 ) se encuentra precedido por un coeficiente diferente de uno (debe ser positivo). Este se trabaja de una manera un poco diferente, la cual detallamos a continuación:
) se encuentra precedido por un coeficiente diferente de uno (debe ser positivo). Este se trabaja de una manera un poco diferente, la cual detallamos a continuación:- Multiplicamos el coeficiente “a” de el factor “a
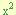 ” por cada termino del trinomio, dejando esta multiplicación indicada en el termino “bx” de la manera “b(ax)”, y en el termino “a
” por cada termino del trinomio, dejando esta multiplicación indicada en el termino “bx” de la manera “b(ax)”, y en el termino “a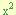 ” de la manera
” de la manera 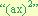 .
.
- Se descompone el trinomio en dos factores binomios cuyo primer termino será la raíz cuadrada del termino
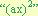 la que seria “ax”.
la que seria “ax”.
- al producto resultante lo dividimos entre el factor “a”, con el fin de no variar el valor del polinomio.
- El signo del primer binomio será el mismo signo que tenga el termino “bx”, el signo del segundo binomio será igual a la multiplicación de los signos de “bx” y de “c”.
- Se buscaran los segundos términos de los binomios según los pasos tres y cuatro del caso del trinomio anterior.
Ejemplo explicativo:
10. VECTOR DIRECTOR

Un vector director es un vector que da la dirección de una recta y también la orienta, es decir, le da un sentido determinado.
En el plano, en el espacio tridimensional o en cualquier espacio vectorial, una recta se puede definir con dos puntos o, de manera equivalente, con un punto y un vector director. En efecto, a partir de dos puntos distintos A y B se obtiene un punto, digamos A, y un vector director u = AB. Recíprocamente, con un punto A de la recta y un vector director u se construye un segundo punto de la misma, definido por AB = u. Esta recta se escribe (AB) o (A, u).

11.Producto escalar:


El producto escalar de dos vectores es una operación que toma dos vectores y produce un número real:

Observemos que el producto escalar se suele denotar por medio de un punto  . Otra notación que se suele utilizar es
. Otra notación que se suele utilizar es  . Sin embargo, en Superprof siempre denotaremos el producto escalar utilizando un punto
. Sin embargo, en Superprof siempre denotaremos el producto escalar utilizando un punto
 . Otra notación que se suele utilizar es
. Otra notación que se suele utilizar es  . Sin embargo, en Superprof siempre denotaremos el producto escalar utilizando un punto
. Sin embargo, en Superprof siempre denotaremos el producto escalar utilizando un punto
Además, el producto escalar no debe confundirse con la multiplicación de un vector por un escalar.
12. COORDENADAS POLARES
Con coordenadas polares señalas un punto diciendo la distancia y el ángulo que se forma:

13. COORDENADAS RECTANGULARES
El sistema de coordenadas rectangulares (o plano cartesiano) es un objeto matemático formado por dos rectas perpendiculares trazadas sobre un plano llamadas "ejes", la recta horizontal es el eje X, la recta vertical es el eje Y. El plano queda dividido en cuatro partes llamados cuadrantes.
14. RECTANGULARES A POLARES
Si tienes un punto en coordenadas cartesianas (x,y) y lo quieres en coordenadas polares (r,θ), necesitas resolver un triángulo del que conoces dos lados.
Ejemplo: ¿qué es (12,5) en coordenadas polares?
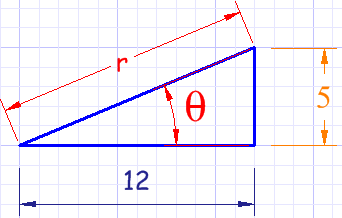
Usamos el teorema de Pitágoras para calcular el lado largo (la hipotenusa):
r2 = 122 + 52
r = √ (122 + 52)
r = √ (144 + 25) = √ (169) = 13
Usa la función tangente para calcular el ángulo:
tan( θ ) = 5 / 12
θ = atan( 5 / 12 ) = 22.6°
Así que las fórmulas para convertir coordenadas cartesianas (x,y) a polares (r,θ) son:
r = √ (x2 + y2)
θ = atan( y / x )
15. COORDENADAS DE POLARES A RECTANGULARES
Si tienes un punto en coordenadas polares (r, θ) y lo quieres en coordenadas cartesianas (x,y) necesitas resolver un triángulo del que conoces el lado largo y un ángulo:
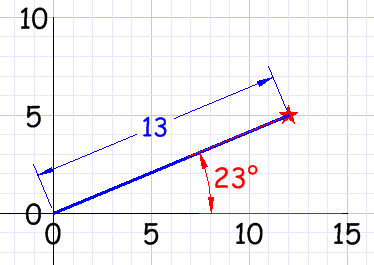
Ejemplo: ¿qué es (13, 23 °) en coordenadas cartesianas?
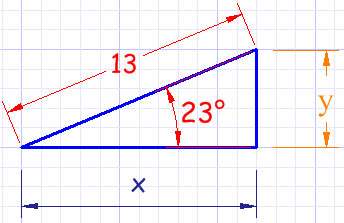
| Usamos la función coseno para x: | cos( 23 °) = x / 13 |
| Cambiamos de orden y resolvemos: | x = 13 × cos( 23 °) = 13 × 0.921 = 11.98 |
| Usamos la función seno para y: | sin( 23 °) = y / 13 |
| Cambiamos de orden y resolvemos: | y = 13 × sin( 23 °) = 13 × 0.391 = 5.08 |
Así que las fórmulas para convertir coordenadas polares (r,θ) a cartesianas (x,y) son:
x = r × cos( θ )
y = r × sin( θ )

Comentarios
Publicar un comentario